Question

On Day 1, there are 256 apples on the tree. On each day after Day 1 until one apple is left the number of apples on the tree is half the number there were the day before. On Day ___, there will be only on apple on the tree

Answer 1

On day 9, there will be only one apple on the tree.

Explanation:

Geometric Sequence

In the geometric sequences, each term is found by multiplying (or dividing) the previous term by a fixed number, called the common ratio.

On day 1, there are 256 apples on the tree.

On the next day, there are half of the apples: 256/2=128 apples

On the next day, there are half of the apples: 128/2=64 apples

This is a geometric sequence with a common ratio of 1/2.

The general formula for the nth term of a geometric sequence is:

`a_n=a_1*r^(n-1)`

Where a1 is the first term and r is the common ratio. We need to find the value of n that results in only one apple in the tree:

`\displaystyle 1=256*\left((1)/(2)\right)^(n-1)`

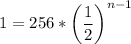
Dividing by 256:

`\displaystyle (1)/(256)=\left((1)/(2)\right)^(n-1)`

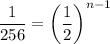
Since
`256=2^8`:

`\displaystyle (1)/(2^8)=\left((1)/(2)\right)^(n-1)`

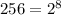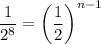
Applying exponents property:

`(1)/(2^8)=\left((1)/(2)\right)^(8)`

`\displaystyle \left((1)/(2)\right)^(8)=\left((1)/(2)\right)^(n-1)`

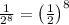
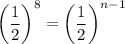
Equating the exponents:

n - 1 = 8

n = 9

On day 9, there will be only one apple on the tree.