Question

Find the base of an isosceles triangle whose area is 60 cm² and the length of one of its equal sides is 13 cm. ​

Answer 1

Base = 24 cm or 10cm

Explanation:

REMEMBER:
An isosceles triangle ABC with base BC = ‘b' & height AD = ‘h' & its equal sides =13 cm & area = 60 cm²

Using the formulas

`A=(bh_b)/(2)`

`h_b=\sqrt{a^2-(b^2)/(4) }`

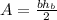
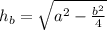
There are 2 solutions for
`b`

`b=2√(2) \frac{A}{\sqrt{a^2+√(a^4-4A^2) } } =2*√(2) *\frac{60}{\sqrt{13^2+√(13^4-4*60^2) } }` ≈
`10cm`
`b=2√(2) \frac{A}{\sqrt{a^2+√(a^4-4A^2) } } =2*√(2) *\frac{60}{\sqrt{13^2-√(13^4-4*60^2) } }=24cm`

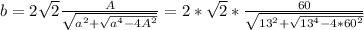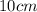
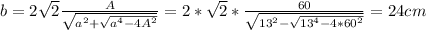
Less complex:

Area of a triangle = 1/2 * b * h = 60

=> h = 120/b

In right triangle ABD

13² = h² + b² /4 ( by Pythagoras law)

=>169 = 120²/b² + b²/4

=>676 b² = 57600 + b^4

=> b^4 - 676 b² + 57600 = 0

=> b² = 676 +- √(676² - 4*57600) / 2

=> b²= 676 +- √(226576) /2

=> b² = (676 +- 476 )/2

=> b² = 1152/2 , 200 /2

=> b² = 576 , 100

=> b = 24, 10

So, Base = 24 cm or 10cm