Question

Which system of equations below has infinitely many solutions?

Oy=-3x + 4 and y=-3x- 4
Oy=-3x + 4 and 3y = -9x+ 12
O y=-3x+4 and y = gx+4
Oy=-3x + 4 and y= -6x + 8


PLEASE HELP!

Answer 1

The system y=-3x + 4 and 3y = -9x+ 12 would contain infinitely many solutions.

Explanation:

Any system of equations that have the same equations would have infinitely many solutions.

In other words, if the two linear equations have the same slope and y-intercept, then the system of solutions would contain infinitely many solutions. So, their graphs would have exactly the same line

Also If the equation ends with a true statement, for instance, 3 = 3, then the system has infinitely many solutions or all real numbers.

Given the system of equations

`y=-3x + 4`

`3y = -9x+ 12`

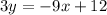
Writing both equations in the slope-intercept form

`y=mx+b`

where m is the slope and b is the y-intercept

y=-3x + 4

Here,

m = -3

b = 4

3y = -9x+ 12

dividing both sides by 3

y = -3x + 4

Here,

m = -3

b = 4

As both equations have the same slope and y-intercept 'b'. Thus, the system of equations has infinitely many solutions.

Now checking:

`\begin{bmatrix}y=-3x+4\\ 3y=-9x+12\end{bmatrix}`

substitute y = -3x+4

`\begin{bmatrix}3\left(-3x+4\right)=-9x+12\end{bmatrix}`

for y = -3x+4

Expressing y in terms of x

`y=-3x+4`

Thus, the solution would contain

`y=-3x+4,\:x=x`

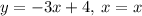
We know that If the equation ends with a true statement, for instance, x = x, then the system has infinitely many solutions or all real numbers.

Thus, the system y=-3x + 4 and 3y = -9x+ 12 would contain infinitely many solutions.