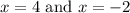Answer:
x = 4 & x = -2
Explanation:
For rational functions (functions which themselves are a fraction, with polynomial pieces in the numerator and polynomial pieces in the denominator), these functions have "discontinuities" anywhere the denominator is equal to zero. Usually, those discontinuities are "vertical asymptotes". Occasionally, those discontinuities are "holes".
A discontinuity is a "hole," only if both the numerator AND the denominator are zero for that same value of x. If that value of x doesn't make the numerator zero (it only makes the denominator zero), the discontinuity is just a vertical asymptote.
Finding the discontinuities:
To find the discontinuities, we'll be making an entirely separate equation. It's not the function, it's not using algebra to change both sides of the equation/function we started with ... it's pretty much just like scratch work to figure out something that you can use later (although, your teacher may want to see your work on how you found them).
The equation we need for this is the denominator of our rational function set equal to zero:
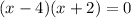
Note, this equation doesn't have a denominator. It's not the original function. It's like scratch work. This equation is designed as if we want the denominator of our function to be zero, and to find the values of x that will make us divide by zero in the original function.
There are many ways to solve this equation. The easiest is remembering the zero product property. The Zero Product property states that if the product of two things is equal to zero, then at least one of the original things had to be zero:
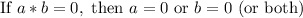
Noting that our equation is a product of two things, and is equal to zero, the zero product property allows us to separate our equation into two equations:
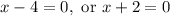
Solving each equation by isolating x, by adding or subtracting the relevant number from both sides of the equations:
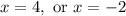
So these values of x will make the denominator of the original function zero. These are both discontinuities of the function, so while when we were solving for values of x that would make the denominator zero, it was appropriate to say "or", we know that both of these values are discontinuities and now we list them both saying "and":
Discontinuities:
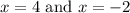
But wait! Are they holes, or are they just vertical asymptotes? Do we have one of each?
Testing to see if the discontinuities are asymptotes:
To test and see if the discontinuities we've found are holes, we need to substitute them into the numerator of the original function, and see the result.... but just the numerator (we already know they will make the denominator zero, and we can't divide by zero)
Since the numerator is just x, we're checking to see if 4=0, or if -2=0. They don't. So, for this function, both of the discontinuities are vertical asymptotes.
Listing the asymptotes
Vertical asymptotes at