Question

Elizabeth deposits a total of $750 into her savings account each year. The account earns 2% interest compounded annually. The table below shows details for the first three years the account was open. How much interest was earned the 4th year?​

Answer 1

Elizabeth earns $ 154.86 due to interests from the beginning to the fourth year and $ 62.75 due to interest only in the fourth year.

Explanation:

Elizabeth deposits each year the same amount, which becomes greater due to composite interest. From statement, we notice the following formulas of recurrence:

Initial amount (
`t = 0`)

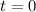`C = C_(o)` (1)

First year (
`t = 1`)

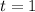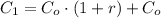`C_(1) = C_(o)\cdot (1+r)+C_(o)` (2)

Second year (
`t = 2`)

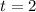`C_(2) = C_(1)\cdot (1+r)+C_(o)` (3)

Third year (
`t = 3`)

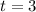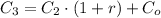`C_(3) = C_(2)\cdot (1+r)+C_(o)` (4)

Fourth year (
`t = 4`)

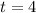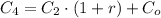`C_(4) = C_(2)\cdot (1+r)+C_(o)` (5)

Where:

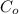`C_(o)` - Initial amount of Elizabeth's account, measured in US dollars.

`r` - Interest rate ratio, dimensionless.

If we know that
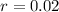`r = 0.02` and
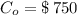`C_(o) = \$\,750`, then the interest earned by Elizabeth in the 4th year is:

First year

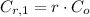`C_(r,1) = r\cdot C_(o)` (6)

`C_(r,1) = (0.02)\cdot (\$\,750)`

`C_(r,1) = \$\,15`

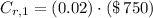
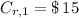
Second year

`C_(1) = C_(o)\cdot (1+r)+C_(o)`

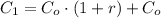
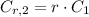`C_(r,2) = r\cdot C_(1)` (7)

`C_(1) = (\$\,750)\cdot (1+0.02)+\$\,750`

`C_(1) = \$ 1515`

`C_(r,2) = (0.02)\cdot (\$\,1515)`

`C_(r,2) = \$\,30.3`

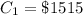
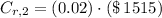
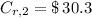
Third year

`C_(2) = C_(1)\cdot (1+r)+C_(o)`

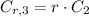`C_(r,3) = r\cdot C_(2)` (8)

`C_(2) = (\$\,1515)\cdot (1+0.02)+\$\,750`

`C_(2) = \$\,2340.75`

`C_(r,3) = (0.02)\cdot (\$\,2340.75)`

`C_(r,3) = \$\,46.81`

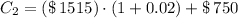
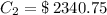
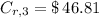
Fourth year

`C_(3) = C_(2)\cdot (1+r) +C_(o)`

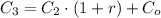
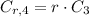`C_(r,4) = r\cdot C_(3)` (9)

`C_(3) = (\$\,2340.75)\cdot (1+0.02)+\$\,750`

`C_(3) = \$\,3137.56`

`C_(r,4) = (0.02)\cdot (\$\,3137.56)`

`C_(r,4) = \$\,62.75`

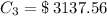
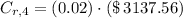
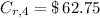
The money gained due to interest is determined by the following sum, that is:

`C_(r) = C_(r,1)+C_(r,2)+C_(r,3)+C_(r,4)`

`C_(r) = \$\,15+\$\,30.30+\$\,46.81+\$\,62.75`

`C_(r) = \$\,154.86`

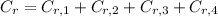
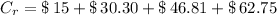
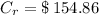
Elizabeth earns $ 154.86 due to interests from the beginning to the fourth year and $ 62.75 due to interest only in the fourth year.