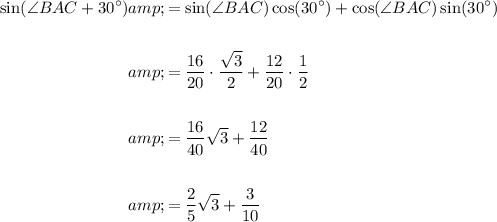Answer:
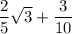
Explanation:
Trigonometric Identities
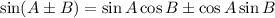
Trigonometric ratios
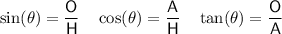
where:
 is the angle
is the angle- O is the side opposite the angle
- A is the side adjacent the angle
- H is the hypotenuse (the side opposite the right angle)
Using the trig ratio formulas for cosine and sine:
Angles

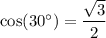
Therefore, using the trig identities and ratios: