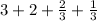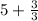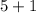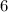Answer:
6
Explanation:
This problem centers on recognizing the relationship between fractions and repeating decimals.
Note the following:
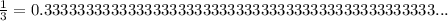
or more simply
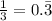
This means that
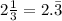
Going back to the original expression,
 simplifies to
simplifies to

Next, adding mixed numbers. For adding mixed numbers, whole number parts and fractional parts can be added separately (this is because of the associative and commutative properties of addition)... because
 means the same thing as
means the same thing as
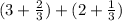
Changing the order, we can write it as
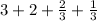
Adding the whole number parts, 3+2 is 5.
Next, adding the fraction parts:
For adding fractions, one must have a common denominator (the bottom part of the fraction must be the same). Once they are the same, the denominator just sort of "hangs out" until the end without changing, and the numerators (the tops) are added together.
Fortunately, the denominators are already the same. So, add the numerators, and the denominator will stay as a 3.
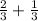
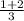
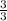
It is important to recognize that any fraction* where the number on the top matches the number on the bottom, the fraction is equivalent to 1.
*(except if the number we're talking about is zero)
So, the fraction parts added together, are equivalent to 1, and the whole number parts added were equal to 5. Returning to our expression...