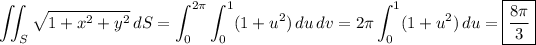Given the parameterization
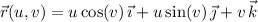
take the normal vector to be
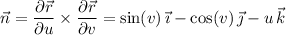
(The order of partial derivatives in the cross product doesn't matter since this a scalar line integral.)
Compute the magnitude of the normal vector.
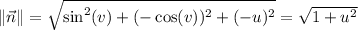
so that the area element reduces to
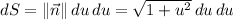
Evaluate the integrand at
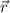 to get
to get
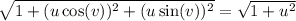
The surface integral reduces to