Question

Determine the time necessary for P dollars to double when it is invested at interest rate r compounded annually, monthly, daily, and continuously. (Round your answers to two decimal places.)

r = 13%

Answer 1

For an interest of 13%, the amount of time it will take the principal to double is:

Annually: About 5.67 years.

Monthly: About 5.36 years.

Daily: About 5.33 years.

Continuously: About 5.33 years.

Explanation:

The standard formula for compound interest is given by:

`\displaystyle A=P(1+(r)/(n))^(nt)`

Where P is the principal, A is the amount afterwards, r is the interest rate, n is the amount of times it is compounded per year, and t is the number of years.

We want to find t for n=1 (annually), n=12 (monthly), n=365 (daily) and continuously when our final amount is double our principal.

In other words, A=2P. Therefore:

`\displaystyle 2P=P(1+(r)/(n))^(nt)`

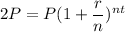
We can divide both sides by P:

`\displaystyle 2=(1+(r)/(n))^(nt)`

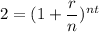
Since our rate is 13%, r=0.13. Hence:

`\displaystyle 2=(1+(0.13)/(n))^(nt)`

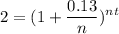
We now have our general formula which we can use to solve.

Annually:

For an annual compound, n=1. Therefore:

`\displaystyle 2=(1+(0.13)/((1)))^((1)t)`

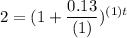
Simplify :

`2=(1.13)^t`

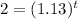
We can take the log (base 10) of both sides:

`\log2=\log1.13^t`

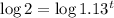
We can move the t in front:

`\log2=t\log1.13`

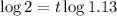
Therefore:

`\displaystyle t=(\log 2)/(\log 1.13)\approx5.67`

So, for an annual compound, it will take about 5.67 years for the principal to double.

Monthly:

For monthly compounds, n=12. Therefore:

`\displaystyle 2=(1+(0.13)/((12)))^((12)t)`

We can take the log of both sides:

`\displaystyle \log 2=\log{(1+(0.13)/(12))^(12t)}`

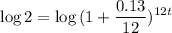
Again, we can move the 12t to the front:

`\displaystyle \log 2=12t\log{(1+(0.13)/(12))`

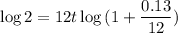
Therefore:

`\displaystyle t=\frac{\log2}{12\log{(1+(0.13)/(12))}}\approx5.36`

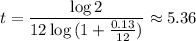
So, for monthly compounds, it will take about 5.36 years for the principal to double.

Daily:

For daily compounds, n=365. Therefore:

`\displaystyle 2=(1+(0.13)/(365))^(365t)\\`

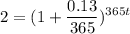
Take the log of both sides and moving the 365t to the front yields:

`\displaystyle \log{2}=365t \log(1+(0.13)/(365))`

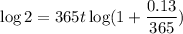
Hence:

`\displaystyle t = ( \log 2)/(365\log(1+(0.13)/(365) ) ) \approx5.33`

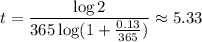
So, for daily compounds, it will take about 5.33 years for the principal to double.

Continuously:

For continuous compound, we will need to use the continuous compound formula:

`A=Pe^(rt)`

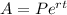
So, A=2P:

`2P=Pe^(rt)`

Dividing both sides by P:

`2=e^(rt)`

Since r=13% or 0.13:

`2=e^(0.13t)`

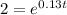
This time, we can take the natural log of both sides:

`\ln2=\ln e^(0.13t)`

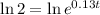
So:

`\ln 2 = 0.13t \ln e`

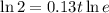
The natural log of e is simply 1. Therefore:

`\ln 2=0.13 t`

Hence:

`\displaystyle t=(\ln 2)/(0.13)\approx5.33`

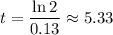
For, for continuously compounded, it will take about 5.33 years for the principal to double.