Answer:
-6 < x < 2
Explanation:
This is the simplest form of absolute value inequality. It can be easily transformed to a "one-step" compound inequality.
__
unfold
The equivalent compound inequality is ...
-4 < x +2 < 4
Subtract 2 to solve:
-6 < x < 2
_____
Additional comment
y = |x +2| means ...
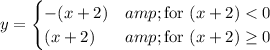
So, writing the equivalent pair of inequalities the "long way", we have ...
x +2 < 4 and (x +2) ≥ 0
and
-(x +2) < 4 and (x +2) ≤ 0
Multiplying the first part of the latter by -1, we can write it as a compound inequality.
(x +2) > -4 and (x +2) ≤ 0 ⇔ -4 < x +2 ≤ 0
Now, our original inequality is two compound inequalities:
-4 < x +2 ≤ 0 and 0 ≤ x +2 < 4
The union of their solution sets is ...
-4 < x+2 < 4