Question

Which binomial is a factor of w^2-w-20

Answer 1

From the given options, option D is the only choice that contains (w-5).

Explanation:

Given the expression

`w^2-w-20`

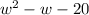
Breaking the expression into groups

`=\left(w^2+4w\right)+\left(-5w-20\right)`

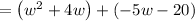
Factor out 'w' form w²+4w = w(w+4)

Factor out 'w' from -5w-20= -5(w+4)

so

`=w\left(w+4\right)-5\left(w+4\right)`

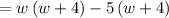
Factor out common term: w+4

`=\left(w+4\right)\left(w-5\right)`

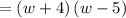
Thus, the factors are: (w+4) and (w-5)

Therefore, from the given options, option D is the only choice that contains (w-5).