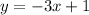Answer:
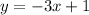
Step-by-step explanation:
Given
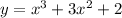
Required
Determine the equation at the point of inflection
The point of inflection of a curve is the point where the second derivative is 0.
So:
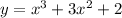
First derivative is:
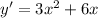
Second derivative:
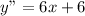
Equate to 0
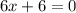
Solve for x
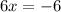
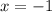
Next, we calculate the slope (m) of the point using the first derivative.
Substitute -1 for x in
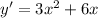
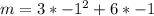
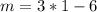
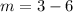
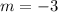
To get the y equivalent;
Substitute
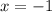 in
in
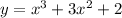
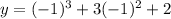
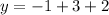
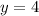
Lastly, we calculate the line equation using:
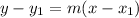
Where
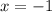 and
and
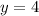
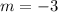
So, we have:
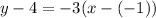
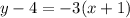
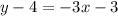
Make y the subject
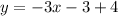
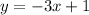
Hence, the equation is: