Question

At a distance of 5.0 m from a point sound source, the sound intensity level is 110 dB. At what distance is the intensity level 95?

Answer 1

The distance of the second sound intensity level is 28.12 m.

Step-by-step explanation:

Given;

intensity of first sound level, I₁ = 110 dB

distance of first sound level, r₁ = 5 m

intensity of second sound level, I₂ = 95 dB

let the distance of second sound level = r₂

The intensity of the sound in W/m² is given as;

`dB = 10 Log[(I)/(I_o) ]`

where;

I₀ is threshold of hearing = 1 x 10⁻¹² W/m²

for 110 dB to W/m²

`110 = 10 Log[(I)/(1 \ * \ 10^(-12)) ]\\\\11 = Log[(I)/(1 \ * \ 10^(-12)) ]\\\\10^(11) = (I)/(1 \ * \ 10^(-12)) \\\\I = 1 \ * \ 10^(-12) \ * \ 10^(11)\\\\I = 10^(-1) \ W/m^2\\\\I = 0.1 \ W/m^2`

for 95 dB to W/m²

`95 = 10 Log[(I)/(1 \ * \ 10^(-12)) ]\\\\9.5 = Log[(I)/(1 \ * \ 10^(-12)) ]\\\\10^(9.5) = (I)/(1 \ * \ 10^(-12)) \\\\I = 1 \ * \ 10^(-12) \ * \ 10^(9.5)\\\\I = 10^(-2.5) \ W/m^2\\\\`

The intensity of sound is related to distance as follows;

`I = (P)/(A) = (P)/(\pi r^2) \\\\I = (1)/(r^2) \\\\I_1r_1^2 = I_2r_2^2 \\\\`

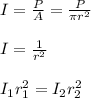
Now, determine the distance of the second sound intensity level

`r_2 ^2 = (I_1r_1^2)/(I_2) \\\\r_2 = \sqrt{(I_1r_1^2)/(I_2) }\\\\r_2 = \sqrt{(0.1 \ * \ 5^2)/(10^(-2.5))}\\\\r_2 = 28.12 \ m`

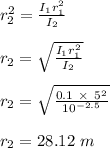
Therefore, the distance of the second sound intensity level is 28.12 m.