Question

The angle of the prism is equal to the angle of minimum deviation for a prism of refractive index 1.414. What is the value of the angle of the prism?

Answer 1

the angle of the prism = 30 degrees

Step-by-step explanation:

The angle of minimum deviation for a prism =

`\mu =(\frac{{sin(A+dm)}/{2}}{sin A/2})`

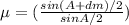
for an equilateral prism, A=60∘

This gives us

`1.414 =(\frac{{sin(60+dm}/{2)}}{sin(60/2)})\\1.414 =(\frac{{sin(60+dm}/{2)}}{0.5})\\0.707 = sin {(60 +dm)/2}\\`

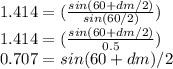
taking the Arcsin of both sides we have

`45 =(60+dm)/(2)\\90 = 60+dm\\dm = 30 degrees`

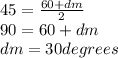
Recall that the angle of the prism is equal to the angle of minimum deviation.

Hence, the angle of the prism = 30 degrees