Answer:
4
Explanation:
Find the limit. Use l’Hospital’s Rule where appropriate. If there is a more elementary method, consider using it. If l’Hospital’s Rule doesn’t apply, explain why?
Given the limit of the function
lim x→[infinity] (4x − ln(x))
Step 1: Substitute x = ∞ into the given function first as shown;
lim x→[infinity] (4x − ln(x))
= (4(∞) − ln(∞))
= ∞ - ∞ (indeterminate)
Step 2: Apply l’Hospital’s Rule
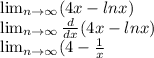
Step 3: Substitute the value of x into the resulting function;
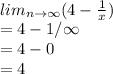
Hence the limit of the function is 4. And yes, the L'hospital rule was applicable.