Question

If a certain amount of ideal gas occupies a volume 8.7 m3 with a pressure of 6 atm and temperature 4.8 oC on earth, what would be its volume on another planet, where the temperature is 8.7oC and the pressure is 7.9 atm ? The answer is in unit of m3

Answer 1

The volume of the ideal gas on another planet will be 6.7 m³.

Step-by-step explanation:

We can find the volume occupied by the ideal gas on another planet by using the Ideal Gas Law:

`PV = nRT`

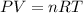
Where:

P: is the pressure

V: is the volume

n: is the number of moles

R: is the gas constant = 8.206x10⁻⁵ m³ atm K⁻¹mol⁻¹

T: is the temperature

Since the gas occupies a volume of 8.7 m³ with a pressure of 6 atm and temperature 4.8 °C on earth, we have the following number of moles:

`n = (PV)/(RT) = (6 atm*8.7 m^(3))/(8.206 \cdot 10^(-5) m^(3)atm/(Kmol)*(4.8 + 273)K) = 2289.9 moles`

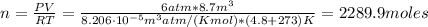
Now we can calculate the volume occupied by the ideal gas on another planet:

`V = (nRT)/(P)`

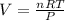
With T = 8.7 °C and P = 7.9 atm

`V = (2289.9 moles*8.206 \cdot 10^(-5) m^(3)atm/(Kmol)*(8.7 + 273)K)/(7.9 atm) = 6.7 m^(3)`

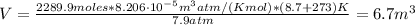
Therefore, the volume of the ideal gas on another planet will be 6.7 m³.

I hope it helps you!