Answer:
Shortest distance from the mountain is 3.17 miles.
Explanation:
From the figure attached,
Let a mountain is located at point A.
Angle between the mountain and point B (∠B) = 53°
Angle between the mountain and point C (∠C) = 78°
Distance between these points = 3 miles
Since, m∠A + m∠B + m∠C = 180°
m∠A + 53° + 78° = 180°
m∠A = 180°- 131° = 49°
By applying sine rule in triangle ABC,
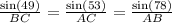
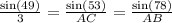
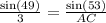
AC =
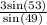
AC = 3.17 miles
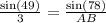
AB =
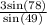
AB = 3.89 miles
Therefore, shortest distance from the mountain is 3.17 miles.