Question

Andre drew a plan of a courtyard at a scale of 1 to 60. On his drawing, one side of the courtyard is 2.75 inches. What is the actual measurement of that side of the courtyard? Express your answer in inches and then in feet. If Andre made another courtyard scale drawing at a scale of 1 to 12, would this drawing be smaller or larger than the first drawing? Explain your reasoning.

Answer 1

1. The actual measurement of the side of courtyard is 165 inches.

ii. The actual measurement of the courtyard is 13.75 feet.

2. The drawing would be larger than the first drawing.

Explanation:

1. Given a scale of 1:60, this implies that 1 unit of measurement on the drawing is equal to 60 units of measurement of the actual courtyard.

scale =
`(length on drawing)/(actual length)`

length on drawing = 2.75 inches, let the actual measurement of the courtyard be represented by y.

So that,

`(1)/(60)` =
`(2.75 inches)/(y)`

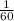y = 60 x 2.75 inches

= 165 inches

The actual measurement of the side of courtyard is 165 inches.

ii. Since,

12 inches = 1 feet

Then,

165 inches = x feet

x =
`(165)/(12)`

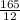
= 13.75 feet

The actual measurement of the courtyard is 13.75 feet.

2. Given the scale of 1:12, the drawing would be bigger than the first drawing. Though both scales are reduced scale.

1:60 implies 60 times less than the actual measurement.

1:12 implies 12 times less than the actual measurement.

Therefore, the second scale (1:12) would make the drawing larger than the first drawing.