Question

A light with frequency of 3.5 x 10^15 Hz is utilized to illuminate the selenium metal (work function 5.11 eV). What will be the maximum velocity of the ejected photoelectrons in 10^6 m/sec?

Answer 1

The maximum speed of the ejected photoelectrons is 1.815 x 10⁶ m/s.

Step-by-step explanation:

Given;

frequency of the light, f = 3.5 x 10¹⁵ Hz

work function of the metal, Φ = 5.11 eV

Φ = 5.11 x 1.602 x 10⁻¹⁹ J = 8.186 x 10⁻¹⁹ J

The energy of the incident light is given as sum of maximum kinetic energy and work function of the metal.

E = K.E + Φ

where;

E is the energy of the incident light, calculated as;

E = hf

E = (6.626 x 10⁻³⁴)(3.5 x 10¹⁵)

E = 2.319 x 10⁻¹⁸ J

The maximum kinetic energy of the photoelectrons is calculated as;

K.E = E - Φ

K.E = 2.319 x 10⁻¹⁸ J - 8.186 x 10⁻¹⁹ J

K.E = 2.319 x 10⁻¹⁸ J - 0.8186 x 10⁻¹⁸ J

K.E = 1.5004 x 10⁻¹⁸J

The maximum speed of the ejected photoelectrons in 10⁶ m/s is given as;

K.E = ¹/₂mv²

`v_(max)^2 = (2K.E)/(m) \\\\v_(max)= \sqrt{(2K.E)/(m)} \\\\v_(max) = \sqrt{(2(1.5 \ * \ 10^(-18)))/((9.11 \ * \ 10^(-31)))}\\\\v_(max) =1.815 \ * \ 10^(6) \ m/s`

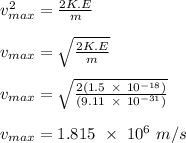
Therefore, the maximum speed of the ejected photon-electrons is 1.815 x 10⁶ m/s.