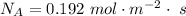Answer:
The value
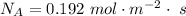
Step-by-step explanation:
From the question we are told that
The thickness of the air is
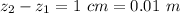
The temperature is
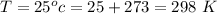
The total pressure is
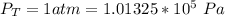
The partial pressure of Ammonia first side is
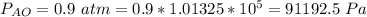
The partial pressure of Ammonia to the second side is
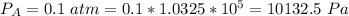
Rate of flow of ammonia is
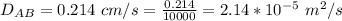
Generally the molar flux of ammonia is mathematically represented as
![N_A = (D_(AB) * P_T )/(RT(z_2 -z_1)) * ln [(P_T - P_(Al))/(P_T - P_(AO)) ]](https://img.qammunity.org/2021/formulas/chemistry/high-school/shq9smtqzp60x7ljsbqp45mlv6m9ku3nqo.png)
Here R is the gas constant with value
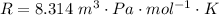
![N_A = (2.14 *10^(-5) * 1.01325*10^(5) )/(8.314 *298 (0.01)) * ln [(1 - 0.1)/(1 - 0.9) ]](https://img.qammunity.org/2021/formulas/chemistry/high-school/v7pnf2ucdtcmcoifau0r8s3fzmt3ffve2k.png)
=>