Question

A box contains 35 gems, of which 10 are real diamonds and 25 are fake diamonds. Gems are randomly taken out of the box, one at a time without replacement. What is the probability that exactly 2 fakes are selected?

Answer 1

`Probability = 0.504`

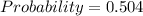
Explanation:

Given

`Gems= 35`

`Real = 10`

`Fake = 25`

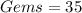
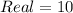
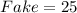
Required

Determine the probability of selecting two fakes

The probability can be represented as thus:
`P(Fake\ and\ Fake)`

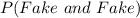
Using the following probability formula, we have:

`P(Fake\ and\ Fake) = P(Fake) * P(Fake)`

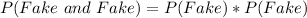
Each probability is calculated by dividing number of fakes by total number of gems:

`P(Fake\ and\ Fake) = (25)/(35) * (25-1)/(35-1)`

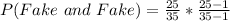
The minus 1 (-1) represent the numbers of fake and total gems left after the first selection

`P(Fake\ and\ Fake) = (25)/(35) * (24)/(34)`

`P(Fake\ and\ Fake) = (5)/(7) * (12)/(17)`

`P(Fake\ and\ Fake) = (60)/(119)`

`P(Fake\ and\ Fake) = 0.504`

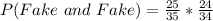
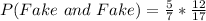
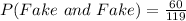
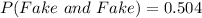
Hence, the required probability is approximately 0.504