Question

A sample of 1700 computer chips revealed that 73% of the chips do not fail in the first 1000 hours of their use. The company's promotional literature claimed that more than 70% do not fail in the first 1000 hours of their use. Is there sufficient evidence at the 0.05 level to support the company's claim?

Answer 1

It is a left tailed test.

Given : n = 1700

`$\hat P = 0.73$`

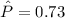
α = 0.05

We want to test,

the null hypothesis,
`$H_0:P=0.70$`

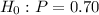
the alternate hypothesis,
`$H_1: P> 0.70 $`

Test statistics is

`$z=\frac{\hat P - P_0}{\sqrt{(P_0(1-P_0 ))/(n)}} $`

`$z=\frac{0.73 - 0.70}{\sqrt{(0.70(1-0.70 ))/(1700)}} $`

`$z=2.70 $`

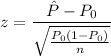
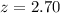
Thus z - critical value = 1.64

Since, z calculated ----- z-critical value

(2.70) (1.64)

Thus we reject the null hypothesis.

So there is sufficient evidence at 0.05 level to support the company's claim that more the 70% do not fail in the first 1000 hours of their use.