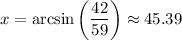You can use the sine law, which states that, in every triangle, the ratio between a side and the sine of the opposite angle is constant.
So, we have

where
 is the angle you're looking for. Now, remember that
is the angle you're looking for. Now, remember that
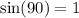 , and we can solve the equation for
, and we can solve the equation for
 :
:
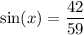
Which implies that the angle itself is