Answer:
I think this is a pretty good question of law of indices
Explanation:
Given that
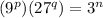
a) express n in terms of p and q ,
b) hence if p = 1 and q = 2 find the value of n
Solution to part a)
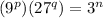
Simplify the equation and how do we do that? As we can see that 9 can also be written as 3^2 and 27 can be written as 3^3 we can rewrite the following equation like this,
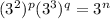
now we multiply p with 2 and
multiply q with 3 respectively,
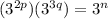
now since the bases are same and are multiplying the exponents will add themselves like this, in this equation the number 3 is the base
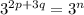
now since the bases on the left hand side and on the right hand side are equal the exponents will also be equal so now,

hence n is expressed in terms of p and q
Solution to part b)
if p = 1 and q = 2 we plug in these values in the above equation we found for n
n = 2p + 3q
n = 2(1) + 3(2)
n = 2 + 6
n = 7