Question

How many moles are in 4.6x1023 molecules of H20 expressed in the correct number

of significant figures?

Answer 1

We know that:

One mole of any element or compound contains 6.022*10²³ atoms/molecules

where 6.022*10²³ is also known as Avogadro's number

So, Number of moles =
`(Number of atoms/molecules)/(Avogadro's number)`

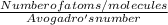
Number of moles in the given sample of H₂O:

From above:

Number of moles = Number of molecules / Avogadro's number

replacing the variables

Number of moles =
`(4.6 * 10^(23))/(6.022*10^(23))`

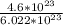
Number of moles =
`(4.6)/(6.022)`

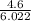
Number of moles = 0.7639 moles

Number of Moles in correct significant Figures:

We know that the number of significant figures of the quotient is the least number of significant figures from the numbers being divided

To find the number of moles, we divided 4.6 by 6.022

Here, 4.6 has 2 significant figures and 6.022 has 4 significant figures

Hence, the quotient(number of moles) will have 2 significant figures

Number of moles in correct significant figures = 0.76 moles