Answer:
a = -6/5
Explanation:
For the graphs to be parallel the graphs should have same slope(m)
So we rewrite both our equations in the slope-intercept form then compare the slope to find the value of a like this,

This equation is the slope-intercept form we convert both our equations in this form firstly taking equation 1
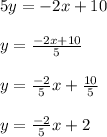
so if we compare it with y = mx + b the coefficient of x is m and hence
m= -2/5 now solving for equation 2
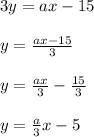
so here if we compare it with y = mx + b the coeffienct of x is a/3 so since parallel lines have same slope by the formula:

we equation both the slope to each other to find the value of a like this,
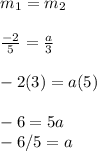
so the value of a equals
a= -6/5