We are given:
The 2 points through which the line passes through
(0,9) and (8,7)
__________________________________________________________
Finding the equation of the line:
To find the equation of the line, we will use the slope-intercept form:
y = mx + b [where m is the slope and b is the y-intercept]
So, we need the slope and the y-intercept of the line in order to find the equation
Finding the slope:
We know that the slope of a line is: change in y / change in x
So, Slope =
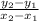
replacing the variables:
Slope = (7-9) / (8-0)
Slope = -2 / 8
Slope = -1/4
Finding the y-intercept:
Since we know the slope, we know that the equation of the line will look like:
y= (-1/4)x + b [where b is the y-intercept]
we know that the ordered pair (0,9) will satisfy the equation since the line passes through that point
So, y = 9 and x = 0 will satisfy the equation:
9 = (-1/4)(0) + b
b = 9
Hence, the y-intercept is 9
Equation of the line:
We know that the general form of the slope-intercept form is:
y = mx + b [where m is the slope and b is the y-intercept]
Since we know the values of the slope and the y-intercept:
y = (-1/4)x + 9
y = -x/4 + 9 is the equation of the line that passes through the given points