Question

A species of fish was added to a lake. The population size P() of this species can be modeled by the following function, where t is the number of years from the

time the species was added to the lake.
P(t)=2000/1+3e^-0.34t
Find the initial population size of the species and the population size after 9 years.
Round your answers to the nearest whole number as necessary.
Initial population size: ?
Population size after 9 years: ?

Answer 1

The initial population size is 500 fish

Population size after 9 years: 1910 fish

Explanation:

Mathematical Model

We usually represent real situations as mathematical functions or rules that express the dependency of one variable quantity P with another variable quantity t.

The population size of a species of fish P(x) is modeled by the following function:

`\displaystyle P(t)=(3000)/(1+3e^(-0.34t))`

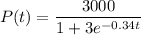
Where t is the number of years elapsed since the species was added to the lake.

The initial population size can be found by substituting t for 0:

`\displaystyle P(0)=(2000)/(1+3e^(-0.34*0))`

`\displaystyle P(0)=(2000)/(1+3*1)`

`\displaystyle P(0)=(2000)/(4)`

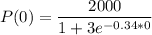
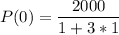
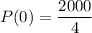
P(0)=500

The initial population size is 500 fish

The population size after t=9 years is:

`\displaystyle P(9)=(2000)/(1+3e^(-0.34*9))`

`\displaystyle P(9)=(2000)/(1+3e^(-3.06))`

`\displaystyle P(9)=(2000)/(1.047)`

`P(9)\approx 1910`

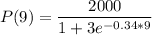
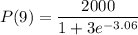
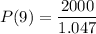
Population size after 9 years: 1910 fish