Answer:
Option C
Explanation:
We solve the system of equations by using the Elimination method as follows,
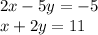
We multiply the second equation with -2 and then add both the equations to eliminate the variable x
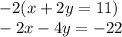
so now,
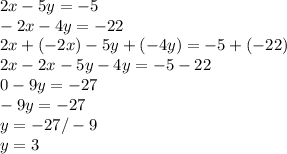
we found the value of y to be y = 3 now we insert this value in any equation of the system either it be the first or the second to calculate the value of x so here goes,
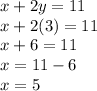
so the solution to the system of equations is (5 , 3) not (10 , 5) which is given in the question even though the ordered pair (10 , 5) satisfies the first equation it is not the solution to the system because in the system it has two equations instead of one so (10 , 5) holds true for the first equation not for the second so Option C is your best answer because it atleast makes one of the equations false.