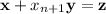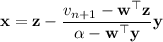(i) Each of u, v, and w are vectors in Rⁿ, so they each have size n × 1 (i.e. n rows and 1 column). So u and v both have size n × 1, while wᵀ has size 1 × n.
M is an n × n matrix, so the matrix A has been partitioned into the blocks
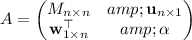
where α is a scalar with size 1 × 1. So A has size (n + 1) × (n + 1).
(ii) Multiplying both sides (on the left is the only sensible way) by the given matrix gives
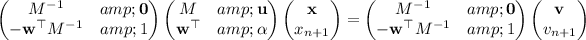
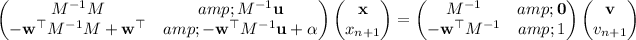
and of course M ⁻¹ M = I (the identity matrix), so
-wᵀ M ⁻¹ M + wᵀ = -wᵀ + wᵀ = 0ᵀ (the zero vector transposed)
(iii) Simplifying the system further gives
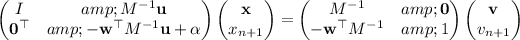
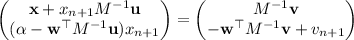
So now, setting y = M ⁻¹u and z = M ⁻¹ v gives
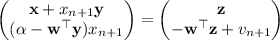
Given that α - wᵀy ≠ 0, it follows that
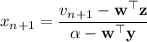
(iv) Combining the result from (iii) with the first row gives