Question

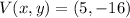
Identify the vertex, axis of symmetry and the max/min value of the function.
y= (1 - 5)^2 – 16

Answer 1

Vertex:
`V(x,y) =(5, -16)`

Axis of symmetry:
`x = 5`

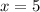
Max/Min value of the function: The minimum value of the curve is -16

Explanation:

The correct statement is now described:

Identify the vertex, axis of symmetry and the max/min value of the function.

`y = (x-5)^(2)-16`

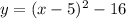
Vertex

Based on the definition of the standard form of the equation of the parabola with a vertical axis of symmetry we can find where the vertex is:

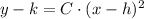`y - k = C\cdot (x-h)^(2)` (1)

Where:

`h`,
`k` - Coordinates of the vertex, dimensionless.

`C` - Constant, dimensionless.

`x`,
`y` - Independent and independent variables, dimensionless.

The standard form of the given equation is:

`y+16 = 1\cdot (x-5)^(2)`

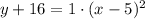
Then, we notice that the vertex of parabola is located at
`V(x,y) =(5, -16)`.

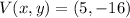Axis of symmetry

In this case, the axis of symmetry corresponds to a vertical line that passes through the vertex. Therefore, the axis of symmetry is represented by
`x = 5`.

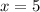Max/Min value of the function

Given that the constant (
`C`) is greater than zero, it means that given parabola contains an absolute minimum represented by the vertex. Then, the minimum value of the curve is -16.