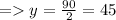Question

Find the measurements of the unknown angles in this figure

Answer 1

x = 30° ; y = 45°

Explanation:

Angle subtended by the diameter on any point of the circle is 90°. So,angleRSP = 90°

angleRST = 120° (given)

But,

angleRST = angleRSP + anglePST

`= > 90 + x = 120`

`= > x = 120 - 90 = 30`

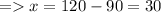
In triangle PQR , PQ = RQ (given)

Hence , it is an isosceles triangle. As it is an isosceles triangle , the base angles are equal.

=> anglePRQ = angleRPQ = y°

anglePQR = 90° (Angle subtended by diameter on any point of circle is 90°)

According to Angle Sum Property of Triangle,

anglePRQ + angleRPQ = anglePQR

`= > 90 + y + y = 180`

`= > 2y = 180 - 90 = 90`

`= > y = (90)/(2) = 45`