Answer:
Option A.
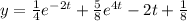
Step-by-step explanation:
This is a second order DE, so we'll need to integrate twice, applying initial conditions as we go. At a couple points, we'll need to apply u-substitution.
Round 1:
To solve the differential equation, write it as differentials, move the differential, and integrate both sides:
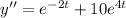
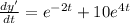
![dy'=[e^(-2t)+10e^(4t)]dt](https://img.qammunity.org/2023/formulas/advanced-placement-ap/high-school/npa91rnf78ghlhykgapxapjhofujeguf59.png)
![\int dy'=\int [e^(-2t)+10e^(4t)]dt](https://img.qammunity.org/2023/formulas/advanced-placement-ap/high-school/gx41qoaqyor7utcejzvgi5qnwb3kqwa2oz.png)
Applying various properties of integration:
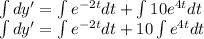
Prepare for integration by u-substitution
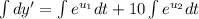 , letting
, letting
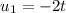 and
and
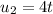
Find dt in terms of
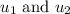
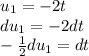
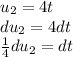
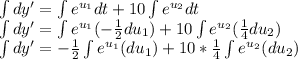
Using the Exponential rule (don't forget your constant of integration):
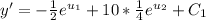
Back substituting for
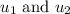 :
:
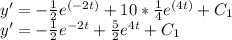
Finding the constant of integration
Given initial condition
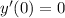
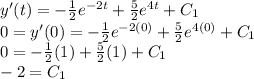
The first derivative with the initial condition applied:
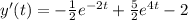
Round 2:
Integrate again:
![y' =-(1)/(2) e^(-2t) + (5)/(2)e^(4t) -2\\(dy)/(dt) =-(1)/(2) e^(-2t) + (5)/(2)e^(4t) -2\\dy =[-(1)/(2) e^(-2t) + (5)/(2)e^(4t) -2]dt\\\int dy =\int [-(1)/(2) e^(-2t) + (5)/(2)e^(4t) -2]dt\\\int dy =\int -(1)/(2) e^(-2t) dt + \int (5)/(2)e^(4t) dt - \int 2 dt\\\int dy = -(1)/(2) \int e^(-2t) dt + (5)/(2) \int e^(4t) dt - 2 \int dt\\](https://img.qammunity.org/2023/formulas/advanced-placement-ap/high-school/x66xy654564du7ixswvioaypi872eh7dlx.png)
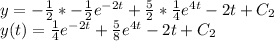
Finding the constant of integration :
Given initial condition

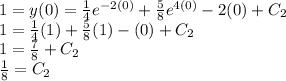
So,
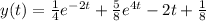
Checking the solution
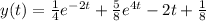
This matches our initial conditions here
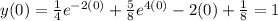
Going back to the function, differentiate:
![y' = [(1)/(4) e^(-2t) + (5)/(8) e^(4t) - 2 t + (1)/(8)]'\\y' = [(1)/(4) e^(-2t)]' + [(5)/(8) e^(4t)]' - [2 t]' + [(1)/(8)]'\\y' = (1)/(4) [e^(-2t)]' + (5)/(8) [e^(4t)]' - 2 [t]' + [(1)/(8)]'](https://img.qammunity.org/2023/formulas/advanced-placement-ap/high-school/ddnrul7a9chqt44oacermsqgd0xwo39dj5.png)
Apply Exponential rule and chain rule, then power rule
![y' = (1)/(4) e^(-2t)[-2t]' + (5)/(8) e^(4t)[4t]' - 2 [t]' + [(1)/(8)]'\\y' = (1)/(4) e^(-2t)(-2) + (5)/(8) e^(4t)(4) - 2 (1) + (0)\\y' = -(1)/(2) e^(-2t) + (5)/(2) e^(4t) - 2](https://img.qammunity.org/2023/formulas/advanced-placement-ap/high-school/9wnqv68dztbj0zzd45y2ltftedu0hwe03e.png)
This matches our first order step and the initial conditions there.
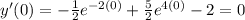
Going back to the function y', differentiate:
![y' = -(1)/(2) e^(-2t) + (5)/(2) e^(4t) - 2\\y'' = [-(1)/(2) e^(-2t) + (5)/(2) e^(4t) - 2]'\\y'' = [-(1)/(2) e^(-2t)]' + [(5)/(2) e^(4t)]' - [2]'\\y'' = -(1)/(2) [e^(-2t)]' + (5)/(2) [e^(4t)]' - [2]'](https://img.qammunity.org/2023/formulas/advanced-placement-ap/high-school/axu38tlxx2e1wjfivnop88758sn69z9y5d.png)
Applying the Exponential rule and chain rule, then power rule
![y'' = -(1)/(2) e^(-2t)[-2t]' + (5)/(2) e^(4t)[4t]' - [2]'\\y'' = -(1)/(2) e^(-2t)(-2) + (5)/(2) e^(4t)(4) - (0)\\y'' = e^(-2t) + 10 e^(4t)](https://img.qammunity.org/2023/formulas/advanced-placement-ap/high-school/qveq8luplw5xzgrae83z3ax00paabquf5w.png)
So our proposed solution is a solution to the differential equation, and satisfies the initial conditions given.