Question

How much should you invest each month in order to have $300,000 if your rate of return is 6.9% compounded monthly and you want to achieve your goal in 40 years?

Answer 1

$39.87

Explanation:

To answer this equation we need to use this equation:

`A = P(1 + (r)/(n) )^n^t`

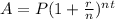
Variable meaning:

A: Amount

P: Initial amount

R: Interest rate (decimal)

N: Number of times interest is compounded per year

T: Time (years)

Given in the question:

A = 300,000

R = .069 (remember that when turning percent to decimal you move the decimal 2 to the left)

N = 12 (because there are 12 months a year)

T = 40 years

Plug into the equation:

`300000 = P(1 + (.069)/(12) )^(^1^2^*^4^0^)`

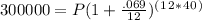
Solve:

`300,000 = P(1 + .00575)^4^8^0\\300,000 = P(1.00575)^4^8^0\\(300000)/((1.00575)^4^8^0) = P\\P = 19138.22`

We aren't done yet, that is the total number of money you need to invest to get $300,000.

Take 19138.22 and divide it by 480 (because there are 480 months in 40 years)

Then you will get 39.87

Therefore, if you invest $39.87 every month for 40 years then the investment should total $300,000.

I hope this helps!

If you think anything is wrong with this let me know!

- Kay :)