Answer:
f(x) = -2(x + 5)²(x - 2)²
Explanation:
Let the function shown by the graph is,
f(x) =
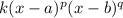
Here, x = a and b are the zeros of the function
p and q are the multiplicity of the function.
If the graph crosses x-axis at a zero x = a, p (multiplicity) will be odd.
If the graph just touches the x-axis at x = b, q will be even.
From the graph attached,
Zeros → x = -5, 2
Graph touches the x-axis, representing the even multiplicity.
Therefore, function will be,
f(x) = k(x + 5)²(x - 2)²
y-intercept from the graph → (0, -200)
From the given function,
-200 = k(0 + 5)²(0 - 2)²
-200 = 100k
k = -2
Therefore, function represented by the graph is,
f(x) = -2(x + 5)²(x - 2)²