Answer:
Explanation:
To prove quadrilateral is a square:
a) Slope of CB
C(-3,-1) ; B = (0,3)
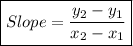
![\sf = (3-[-1])/(0-[-3])\\\\ =(3+1)/(0+3)\\\\ = (4)/(3)](https://img.qammunity.org/2023/formulas/mathematics/high-school/bfmc6ekm2een7yvk7adk2uo06aggfmqtgx.png)
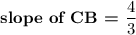
b) D(1,-4) ; A(4,0)
![Slope \ of \ DA = (0-[-4])/(4-1)\\](https://img.qammunity.org/2023/formulas/mathematics/high-school/wdw7xxdd3t5cw7wv97qkyxv785jxuadx1n.png)
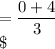
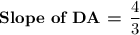
Slope of CB = slope of DA
c) C(-3,-1) ; D(1 , -4)
![\sf Slope \ of \ CD =(-4-[-1])/(1-[-3])](https://img.qammunity.org/2023/formulas/mathematics/high-school/o5jedym96s1x1tu848i0kyl7rk8iumknzq.png)


So, CD is perpendicular to CB
d) B(0,3) ; D(1,-4)
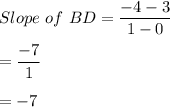
e) C(-3,-1) ; A(4,0)
![\sf Slope \ of \ CA = (0-[-1])/(4-[-3])\\](https://img.qammunity.org/2023/formulas/mathematics/high-school/tqgx5xleiz73qla2bji1fatj6kowfr1oen.png)
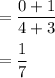

So, CA is perpendicular to BD
