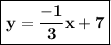Question

What is the equation of the line that is parallel to the line y = -1/3x+4 and passes through the point (6,5)

Answer 1

`\sf y =(-1)/(3)x + 7`

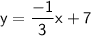
Explanation:

Equation of line: y =mx +b

Here, m is the slope and b is the y-intercept.

Parallel lines have same slope.

`\sf y =(-1)/(3)x + 4`

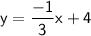
So, the slope of the required line = -1/3

Equation of the required line:

`\sf y =(-1)/(3)x + b`

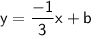
Point(6,5) goes through the line. substitute x = 6 and y =5 in the above equation and then we can find the value of y-intercept 'b'

`\sf 5 =(-1)/(3)*6 +b\\\\ 5 = -2 + b\\\\5+2 = b\\\\\boxed{b = 7}`

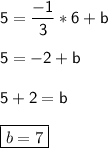
Equation of the require line:

`\sf \boxed{\bf y =(-1)/(3)x+7}`