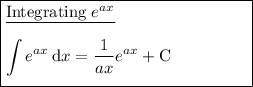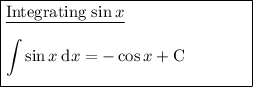Question

Using separation of variables technique, solve the following differential equation with initial condition y'= e sinx and y(pi) = 0. The solution is: ​

Answer 1

`\textsf{A.} \quad e^(-y)=\cos x+2`

Step-by-step explanation:

Given differential equation and initial condition:

`\begin{cases}y'=e^y \sin x\\y(-\pi)=0\end{cases}`

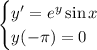
Rearrange the differential equation so that all the terms containing y are on the left-hand side, and all the terms containing x are on the right-hand side:

`y'=e^y \sin x`

`(dy)/(dx)=e^y \sin x`

`(1)/(e^y)\; dy=\sin x\; dx`

`e^(-y)\; dy=\sin x\; dx`

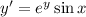
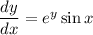
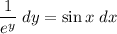
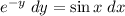
Integrate both sides of the equation:

`\begin{aligned}\displaystyle \int e^(-y)\; dy&=\int \sin x\; dx\\\\-e^(-y)&=-\cos x+C\end{aligned}`

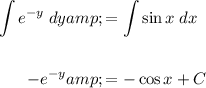
Substitute the given condition y(-π) = 0 into the equation and solve for C:

`\begin{aligned}-e^(-0)&=-\cos (-\pi)+C\\\\-1&=1+C\\\\C&=-2\end{aligned}`

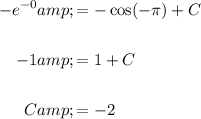
Substitute the found value of C into the equation:

`-e^(-y)=-\cos x-2`

Multiply both sides by -1:

`\boxed{e^(-y)=\cos x+2}`

`\hrulefill`

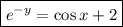
Integration rules used:

`\boxed{\begin{minipage}{5.1 cm}\underline{Integrating $e^(ax)$}\\\\$\displaystyle \int e^(ax)\:\text{d}x=(1)/(ax)e^(ax)+\text{C}$\\\end{minipage}}`

`\boxed{\begin{minipage}{5.1 cm}\underline{Integrating $\sin x$}\\\\$\displaystyle \int \sin x\:\text{d}x=-\cos x+\text{C}$\\\end{minipage}}`