Question

Radicals and complex numbers

Answer 1

`A=8\\\\B=7`

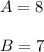
Explanation:

Simplify the radicand by splitting the number into two numbers, one of which is a perfect square (like 4, 9, 16, 25, 36, 49, 64, 81, 100*).

Factors of 448 that include a perfect square: 7 and 64**. Split:

`√(448) \\\\√(64*7)\\\\√(64)*√(7)\\\\ 8√(7)`

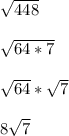
Therefore, A is 8 and B is 7.

:Done

Notes:

*Perfect squares:

`√(4) =2\\\\√(9)=3\\\\√(16)=4\\\\√(25)=5\\\\√(36)=6`
`√(49)=7\\\\√(64)=8\\\\√(81)=9\\\\√(100) =10`

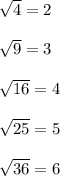
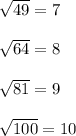
Make sure to use the number in the radical symbol, not the simplified number.

**You can find factors with a perfect square by dividing the radicand by perfect squares. The bigger the number, the better. I started at 100:

448÷100=4.48

448÷81=5.530864197

448÷64=7

Stop when you find one that results in a whole number, like 7. The result and perfect square are the factors.