Question

Suppose a bag contains many marbles, 54% of which are purple. You draw 5 marbles from the bag with replacement.

(a) Find the probability that you draw exactly 2 purple marbles

(b) Find the expected value of the number of purple marbles.

Answer 1

Part A

Use the binomial probability distribution formula.

p = 0.54 = probability of getting a purple marble

n = 5 = sample size

x = 2 = number of purple we want to get

`P(x) = (n!)/(x!(n-x)!)*p^x*(1-p)^(n-x)\\\\P(2) = (5!)/(2!(5-2)!)*0.54^2*(1-0.54)^(5-2)\\\\P(2) = 10*0.54^2*0.46^3\\\\P(2) = 0.283831776\\\\`

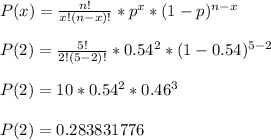
The
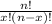`(n!)/(x!(n-x)!)` portion is from the nCr combination formula. The exclamation marks indicate a factorial.

Alternatively, you could use Pascal's Triangle for that portion.

Answer: 0.283831776

This decimal value is exact. Round it however you need to.

============================================================

Part B

To find the expected value, aka the mean, we multiply the sample size and probability of getting a purple marble on any single selection.

n*p = 5*0.54 = 2.7

Answer: 2.7