Answer:
The student is not correct.
Explanation:
A function h(x) is the inverse of f(x) if and only if:
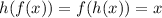
We have that f(x)=4x.
And h(x)=-4x.
Let’s verify whether or not they are inverses using the above property.
So:
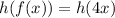
Therefore:
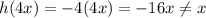
Likewise:

Then:
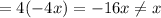
Since both of the compositions do not result in x, the two functions are not inverses.