Question

Please Help!! The variables y and x have a proportional relationship, and y = 9 when x = 2. What is the value of y when x = 3? Enter your answer in the box.

Answer 1

`y=27/2\text{ or } 13.5`

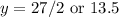
Explanation:

If y and x have a proportional relationship, then they have the standard form:

`y=kx`

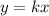
Where k is the constant of proportionality.

We know that y=9 when x=2. So, we can solve for our k. Substitute 9 for y and 2 for x. Hence:

`9=2k`

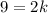
Divide both sides by 2:

`\displaystyle k=(9)/(2)=4.5`

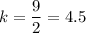
So, our constant of proportionality is 9/2 or 4.5.

Therefore, our equation is:

`\displaystyle y=(9)/(2)x`

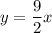
To find y when x=3, substitute 3 for x and evaluate. Hence:

`\displaystyle y=(9)/(2)(3)`

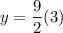
Evaluate:

`\displaystyle y=(27)/(2)=13.5`

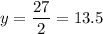
So, when x=3, y=27/2 or 13.5