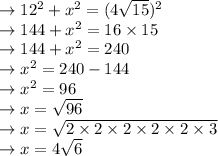Question

Please help solve the question in the picture! Find x

Answer 1

4√6

Explanation:

On the below image, I labeled the 4 points A, B, C, and D. In this diagram, ΔABC is similar to ΔADB and ΔBDC.

Let's look at ∠C here, and find the ratio from the leg adjacent to ∠C and the hypotenuse in 2 triangles, ΔABC and ΔBDC. I chose these as they both share ∠C. You could do the same with ∠A, choosing ΔADB instead.

ΔABC:
`(BC)/(AC)=(BC)/(AD+DC)`

ΔBDC:
`(DC)/(BC)`

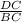
This is just the longer leg over the hypotenuse as said above. Because these triangles are similar, these ratios must be the same. We can write an equation to show that:

`(BC)/(AD+DC)=(DC)/(BC)`

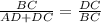
In order to find BD, we first need to find either of the legs in ΔABC. I'll go for BC here as it looks like it'd be the easiest to solve for in this equation. Cross multiply:

`\rightarrow (BC)/(AD+DC)=(DC)/(BC)\\\rightarrow BC* BC = DC*(AD+DC)\\\rightarrow (BC)^2=DC*(AD+DC)`

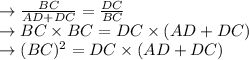
At this point, you can plug in the given values for AD and DC, then solve for BC.

`\rightarrow (BC)^2=12*(8+12)\\\rightarrow (BC)^2=12*20\\\rightarrow (BC)^2=240\\\rightarrow BC=√(240)\\\rightarrow BC=√(2*2*2*2*3*5)\\\rightarrow BC=4√(15)`

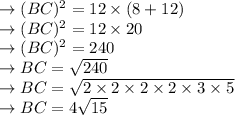
Finally, you can use the pythagorean theorem to find x in ΔBDC.

`\rightarrow 12^2+x^2=(4√(15))^2\\\rightarrow 144+x^2=16*15\\\rightarrow 144+x^2=240\\\rightarrow x^2=240-144\\\rightarrow x^2=96\\\rightarrow x=√(96)\\\rightarrow x=√(2*2*2*2*2*3)\\\rightarrow x=4√(6)`

Answer 2

• C. 4√6

Explanation:

According to the altitude theorem:

• x² = 8*12
• x² = 96
• x = √96
• x = 4√6

Correct choice is C