Question

Select the function that has been shifted up by 2 and is less steep than the function f(x) = 3x-5

---------------------
Answers
A - g (x) = 2x + 2
B - g (x) = 4x -3
C - g (x) = x - 3
D - g (x) = x - 7

Answer 1

As the function has been shifted up by 2 and is less steep than the function f(x) = 3x-5.

Thus, option C is true. i.e. g(x)=x-3

Explanation:

Given the function

`f(x) = 3x-5`

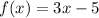
writing in the slope-intercept form

`y = mx+b`

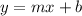
where m is the line and b is the y-intercept

• Thus, slope of f(x) = 3

To move a function up, we need to add outside the function.

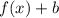`f(x) + b` means
`f(x)` moved up 'b' units.

So, by shifting up by 2 means f(x) would become g(x)= 3x-5+2 = 3x-3

But, we have to find the function which is less steep, meaning having a slope less than 3.

so, the best-suited function that has been shifted up by 2 and is less steep than the function f(x) = 3x-5 will be:

• g (x) = x - 3

A graph is also attached.

• In the graph, the red line represents f(x)=3x-5, and the blue line is representing the function g(x)=x-3 which has been shifted up by 2 and is less steep than the function f(x) = 3x-5.

As the function has been shifted up by 2 and is less steep than the function f(x) = 3x-5.

Thus, option C is true.