Answer:
solving the inequality:
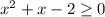 we get
we get
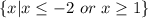
Option A is correct option
Explanation:
We need to solve the inequality:
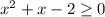
We can solve using factors:
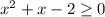
We will break the middle term, in such way that their sum is equal to middle term and product is equal to product of first and last term.
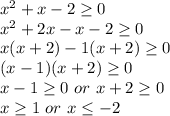
So, solving the inequality:
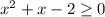 we get
we get
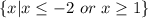
Option A is correct option