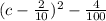Question

Complete the square to make a perfect square trinomial. Then, write the result as a binomial squared.

Answer 1

Perfect squared trinomial is:
`(c-(2)/(10))^2- (4)/(100)`

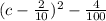
Explanation:

We need to Complete the square to make a perfect square trinomial.

`c^2-(2c)/(5)`

For making it a perfect square it should be of form:
`a^2-2ab+b^2`

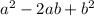
Looking at the given term it can be written as:

`c^2-(2c)/(5)\\=c^2-2(c)((2)/(10))`

So, we have to add (2/10)^2 on both sides

`=c^2-2(c)((2)/(10))+((2)/(10))^2-((2)/(10))^2\\=(c-(2)/(10))^2- ((2)/(10))^2\\=(c-(2)/(10))^2- (4)/(100)`

So, perfect squared trinomial is:
`(c-(2)/(10))^2- (4)/(100)`