The equation of the line passing through the given points is y =
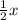 .
.
To find the equation of the line passing through the given points, we can use the slope-intercept form of a linear equation:
![\[ y = mx + b \]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/wtsqddmv4ciat8euuj6md8p7n5le92wt38.png)
where m is the slope and b is the y-intercept.
First, calculate the slope m using two of the given points, for example, (2,1) and (10,5):
![\[ m = \frac{{\text{{change in }} y}}{{\text{{change in }} x}} \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/567zcyds73g8iv4c0h9brhgu3xeaoxymad.png)
![\[ m = \frac{{5 - 1}}{{10 - 2}} = (4)/(8) = (1)/(2) \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/jdsyzj3ffidmalsgaijbo3ug5hyhp1odr7.png)
Now that we have the slope
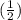 , we can use it in the slope-intercept form and substitute one of the points to find the y-intercept b.
, we can use it in the slope-intercept form and substitute one of the points to find the y-intercept b.
Let's use the point (2,1):
![\[ 1 = (1)/(2)(2) + b \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/s6baoydsq6k83zt9q2vy5f00w38exkcumr.png)
Solve for b:
![\[ 1 = 1 + b \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/yxvgjyen3bx4fo1hrbz1i1knv753gekzny.png)
![\[ b = 0 \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/8qyebt8j0fcp1eim2jeb7jyfpb5g3sc9hh.png)
Now we have the slope
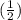 and the y-intercept 0, so the equation of the line is:
and the y-intercept 0, so the equation of the line is:
![\[ y = (1)/(2)x \]](https://img.qammunity.org/2021/formulas/mathematics/high-school/ucd13jm8ujqh2pnzdj6x0i57f6svmmub88.png)
Therefore, the equation of the line passing through the given points is y =
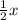 .
.