Answer:
Explanation:
Discriminant:
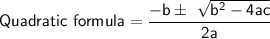
Discriminant is the part of the quadratic formula inside the square root. It determines whether the quadratic equation has real roots or not.
Discriminant = b² - 4ac
Here b is the coefficient of x ; a is the coefficient of x² and c is the constant.
- If b² - 4ac > 0 then the quadratic equation has two distinct real roots.
- If b² - 4ac = 0, then the quadratic equation has two equal real roots.
- If b² - 4ac <0, then the quadratic equation has no real roots.