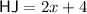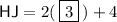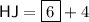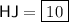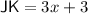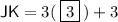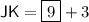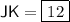Question

Suppose to that J is between H and K. If HJ = 2x + 4, JK = 3x + 3, and KH = 22, find the lengths of HJ and JK. Remember to always draw an image first and to pay attention to what the question is asking for!

(Use the segment addition postulate and then substitute what we know. Do not use any spaces in your answers.) (I can't include any more of the picture sorry, I am giving 45 points for this answer!) ​

Answer 1

HJ = 10

JK = 12

Explanation:

Given:

• HJ = 2x + 4
• JK = 3x + 3
• HK = 22

If J is between H and K, then:

`\sf HJ + JK = \boxed{\sf HK}`

`(\: \boxed{2x+4}\:)+(\:\boxed{3x+3}\:)=\boxed{22}`

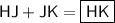
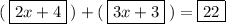
Find x

Once we combine our like terms we get:

`\boxed{5}\:x+\boxed{7}=\boxed{22}`

Subtract 7 from both sides:

⇒ 5x = 15

Divide both sides by 5:

`x=\boxed{3}`

To find HJ and JK, plug in the found value of x into the expressions for HJ and JK:

`\textsf{HJ}=2x+4`

`\textsf{HJ}=2(\:\boxed{3}\:)+4`

`\textsf{HJ}=\boxed{6}+4`

`\textsf{HJ}=\boxed{10}`

`\textsf{JK}=3x+3`

`\textsf{JK}=3(\:\boxed{3}\:)+3`

`\textsf{JK}=\boxed{9}+3`

`\textsf{JK}=\boxed{12}`