Question

. A motorist is speeding along at 33m/s when he sees a squirrel on the road 200 meters in

front of him. He tries to stop, but it takes 12 seconds for his car to stop
(a) What is the acceleration of the car? (assume acceleration was constant)
(b) Does the squirrel survive?
(c) How fast was the car moving at 100 meters?​

Answer 1

Hello!

a)

Use the kinematic equation to solve for the acceleration:

`v_(f) = v_(i) + at`

In this instance, the final velocity is 0 because he comes to a stop. We can solve for the acceleration by plugging in the given values:

0 = 33 + (12)a

0 = 33 + 12a

-33 = 12a

-33 / 12 = a --> a = -2.75 m/s²

b) Find the amount of distance necessary to stop. Use the formula:

`v_(f) ^(2) = v_(i) ^(2) + 2ad`

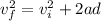
Plug in the values:

0² = 33² + 2(-2.75 · d)

0 = 1089 - 5.5d

-1089 = -5.5d

d = 198 meters. Therefore, the squirrel would survive.

c)

Find the velocity at 100 meters by using the same formula as before:

`v_(f) ^(2) = v_(i) ^(2) + 2ad`

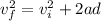
However, in this instance, we are solving for the final velocity. Plug in the given points to solve:

vf² = 33² + 2(-2.75 · 100)

vf² = 1089 + (-550)

vf² = 539

vf = √539

vf ≈ 23.22 m/s.